Hi everyone, and welcome back! In our last adventure (see link), we dove deep into the fascinating world of self-attention, a game-changing mechanism introduced in the Transformer paper by Vaswani et al. We explored how it enables models to weigh the importance of different parts of input data. Today, we're taking that knowledge a step further by unraveling the mysteries of multi-head attention. Why settle for one perspective when you can have multiple? Let's discover how this powerful technique amplifies our Transformer models, allowing them to capture a richer, more nuanced understanding of data.
Why Do We Need Multi-Head Attention?
Multi-head attention boosts a model's capacity by exploring different parts of the input data. To understand this, let’s use a simple analogy, as shown in the following figure.
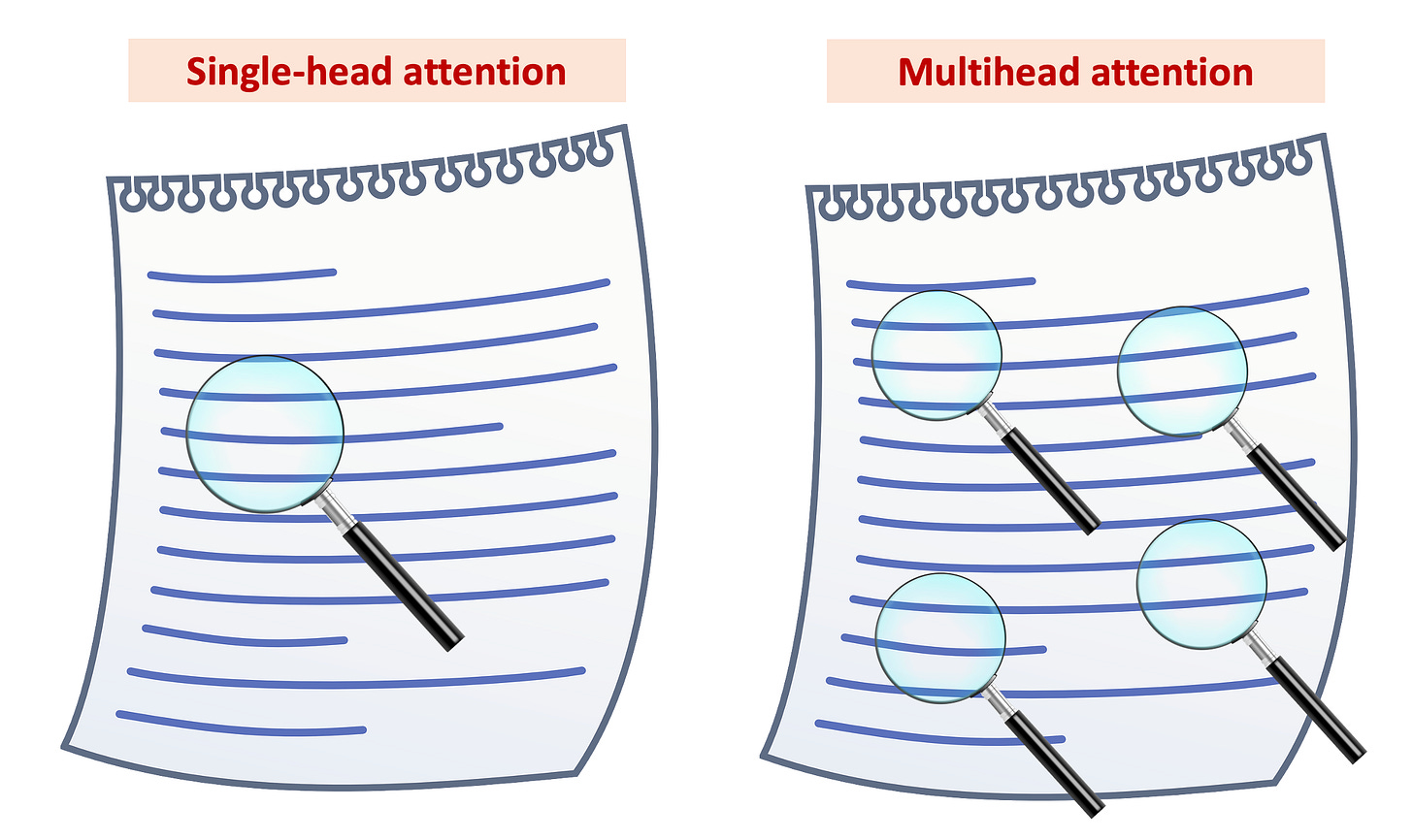
Imagine you have some text. With single-head attention, represented by one magnifier in the right, the model focuses on one part of the text. It's like having one expert analyze the passage. Now, let’s consider the second image on the right with four magnifiers. This is multi-head attention. Each magnifier, or 'head', looks at a different part of the same text. It's like having a team of experts, each examining a separate aspect. This way, the model gets a fuller, more diverse understanding, similar to how multiple experts provide a well-rounded analysis.
Unraveling the Mechanics of Multi-Head Attention
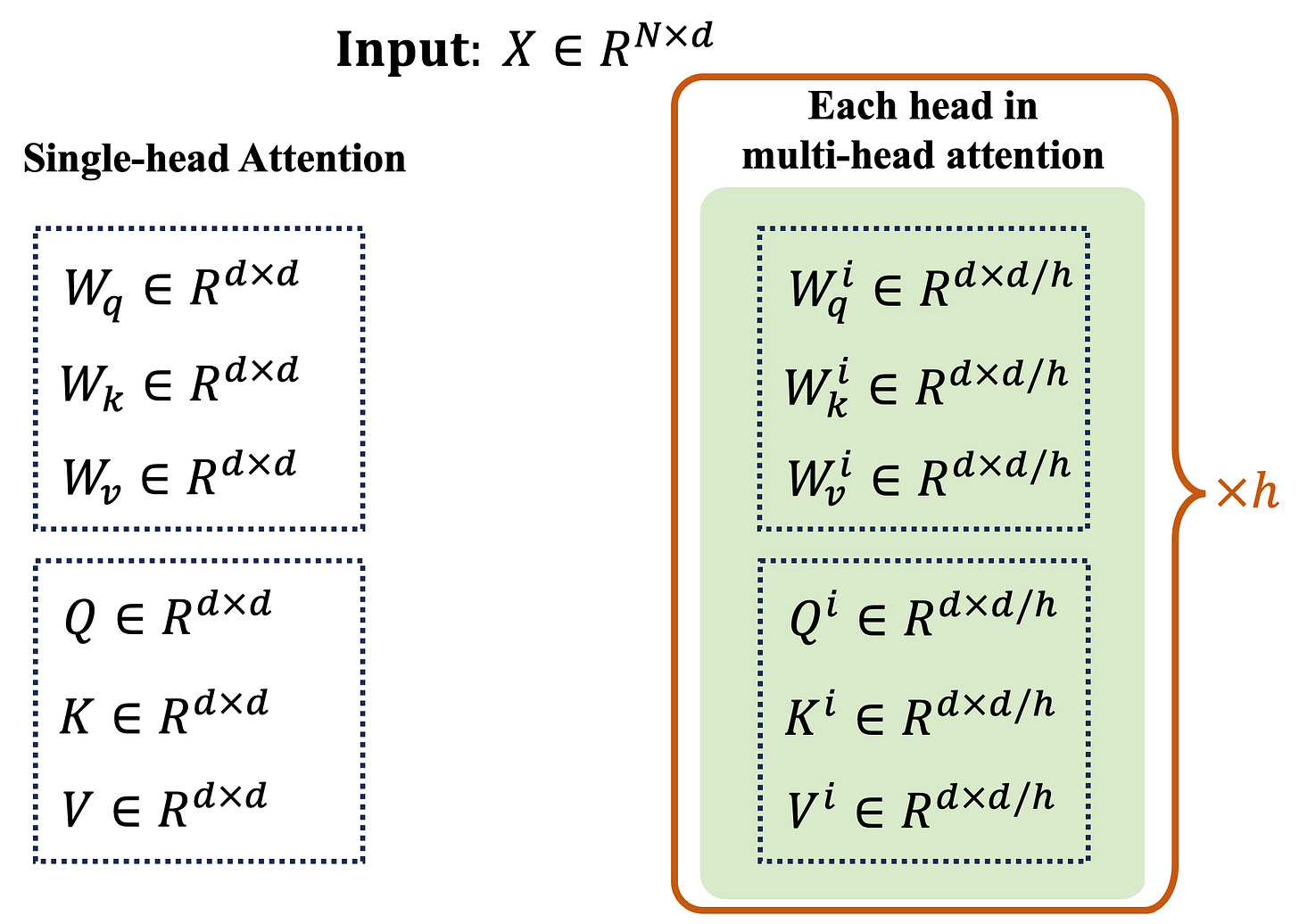
In multi-head attention, the magic happens by running N single-head attentions simultaneously and on smaller query, and value matrices. First step, we need to obtian these smaller query, key, and value matrices. In single-head attention, we transformed X using three weight matrices Wq, Wₖ, and Wᵥ to get our query, key, and value., that is Q=XWqᵀ, K=XWₖᵀ, and V=XWᵥᵀ. so each matrix has size N×d. Using these matrcies, we can split them into h equal parts. This division also helps with the computational efficiency. But, instead of building these full matrices, and then splitting them, we can build them directly from X as we will explain next.
In the multi-head scenario, things get more interesting. We now have h sets of these matrices – Wq¹, Wq², ..., Wqʰ for queries, Wₖ¹, Wₖ², ..., Wₖʰ for keys, and Wᵥ¹, Wᵥ², ..., Wᵥʰ for values. So, in total, we're using 3h weight matrices, each with dimensions of d×(d/h). The process of obtaining queries, keys and values for each head is illustared in the following figure.
Note that despite increasing the number of matrices, we maintain the same number of parameters as a single attention head. This balance keeps our model efficient while vastly expanding its ability to understand and interpret data from multiple perspectives.
Deciphering the Attention Mechanism in Each Head
In the next step, we apply the attention mechanism independently to each head as shown below:
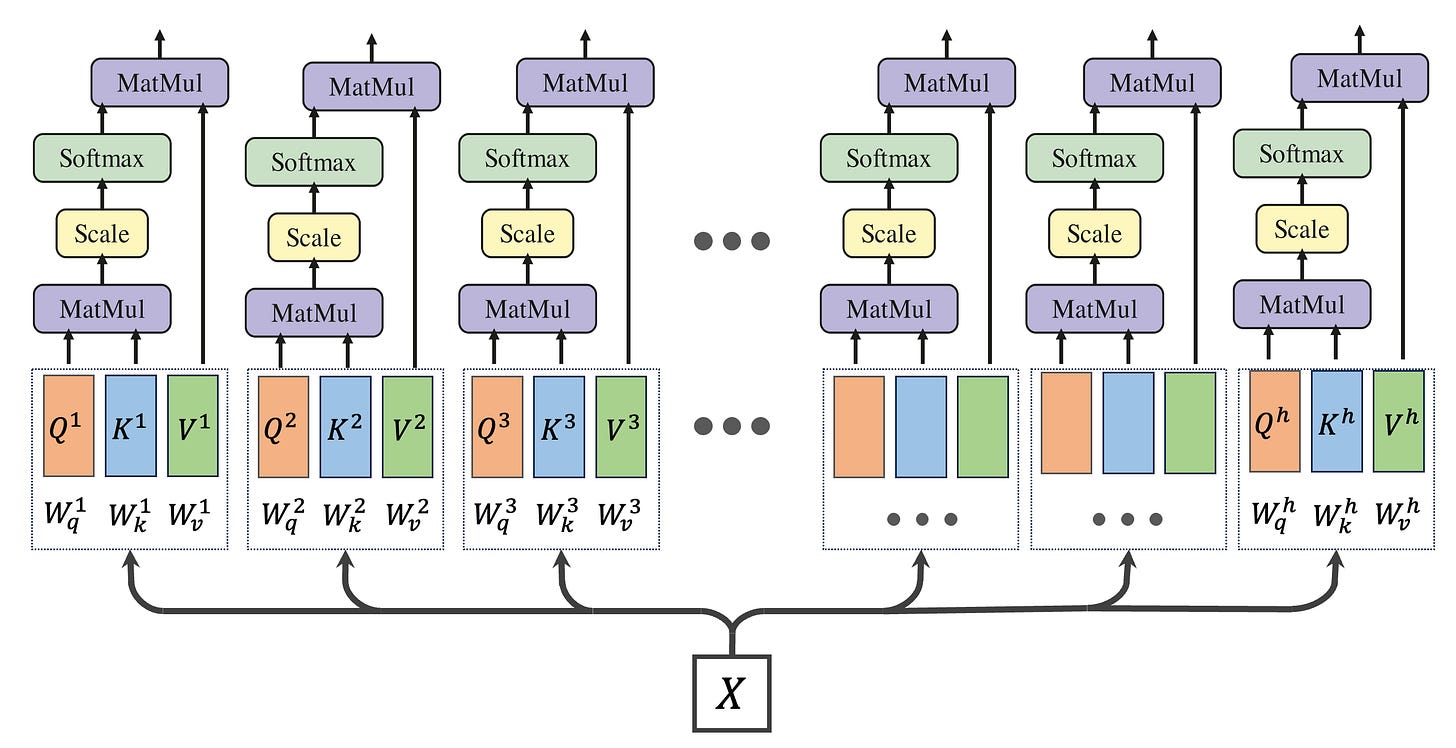
The process involves computing the softmax attention separately for each head. This is captured in the following expressions:
Here, each individual output i (where i ranges from 1 to h) has the size N×(d/h),.
Moving forward, these individual outputs are concatenated. This concatenation is then followed by a matrix multiplication step, which serves to mix these outputs and restore their dimensionality to the original N×d format. This can be represented as:
where Wᴼ is the weight matrix with size d×d, and O is the final output of the multi-head attention with dimensionality N×d.
Conclusion
In this article, we delved into the inner-workings of multi-head attention (MHA), uncovering its advantages over single-head attention. By enabling models to perceive data from multiple perspectives, MHA opens doors to understanding complexities in ways that were previously unattainable with single-head approaches.
For those who enjoy learning through visual means, I've created a detailed video on this topic. Check it out on YouTube here:
Your thoughts and feedback are invaluable - feel free to share them in the comments below. Are there any other deep learning concepts you're curious about? Let me know, and stay tuned for more insights into the fascinating world of AI and machine learning.
Until next time, keep exploring the endless possibilities of deep learning!


This is a great write-up. I like the intuition with the magnifying glass. I also usually tend to think of it as analogous to using multiple channels in a convolutional layer.